Teknolojinin gelişmesiyle birlikte sıkıştırılmamış bir görüntünün saklanması veya transferi zorluk derecesini yitirmemiştir. Görüntünün kodlanması ve sıkıştırılması konusunda ilk andan itibaren çalışmalar halen devam etmektedir. Yapılan çalışmalar hep daha fazla sıkıştırma oranı ve daha iyi görüntü kalitesini yakalamak içindir. Mevcut sistemlerde en çok kullanılan sıkıştırma tekniği Ayrık Kosinüs Dönüşümü (DCT) tabanlı sıkıştırma teknikleridir. Ancak dalgacık tabanlı sıkıştırma tekniğinin DCT tabanlı sıkıştırma tekniğine göre avantajları göz önünde bulundurulduğunda, ileride dalgacık tabanlı sıkıştırmanın çok daha popüler olacağı değerlendirilmektedir. Ben bu çalışmamda DCT üzerine durup uygulama yapacağım.
Veri sıkıştırma yöntemleri, verilerin saklama ortamlarında daha az yer işgal etmeleri için ve bir iletişim ağı üzerinden daha hızlı transfer edilebilmeleri için yaygın olarak kullanılmaktadırlar. Son yıllarda disk kapasitelerinin hızlı bir şekilde artması, genel amaçlı sıkıştırma uygulamalarının kullanımını azalttıysa da, aslında sabit disklerimizde sakladığımız ses, görüntü ve hareketli görüntü dosyalarının tamamına yakını çeşitli yöntemlerle sıkıştırılmış haldedir.
Veri sıkıştırma yöntemleri, sıkıştırma biçimlerine göre kayıplı sıkıştırma yöntemleri ve kayıpsız sıkıştırma yöntemleri olmak üzere ikiye ayrılırlar.
Kayıplı sıkıştırma yöntemleri, verinin bütünlüğünü en az düzeyde etkileyecek olan veri kümelerini çıkartarak, geriye kalan veri kümelerinin de kayıpsız sıkıştırmaya tâbi tutulması temeline dayanır. Bir veri kayıplı bir sıkıştırma yöntemi ile sıkıştırılırsa, verinin tamamı değil, sadece belirli bir kısmı geri getirilebilir. Veri birebir aynı şekilde geri getirilemediği için bu tür yöntemlere kayıplı yöntemler denir.
Kayıpsız sıkıştırma yöntemleri, orijinal veri ile sıkıştırıldıktan sonra geri getirilecek olan verinin tamamıyla aynı olmasının gerekli olduğu durumlarda kullanılır. Örneğin metin tipinde veriler kayıpsız olarak sıkıştırılmalıdırlar, çünkü geri getirildiklerinde kelimelerinde veya karakterlerinde eksiklikler olursa, metnin okunabilirliği azalacak ve hatta anlam kayıpları meydana gelebilecektir.
Veri sıkıştırma yöntemlerini uygulama alanlarına göre sınıflandıracak olursak:
Metin ve ikili tabanlı veri sıkıştırma alanında, her bit değerli olduğu için kayıpsız yaklaşımların kullanılması şarttır.
Ses verisi sıkıştırma alanında, iyi sıkıştırma oranları sağladığı için genellikle kayıplı yaklaşımlar tercih edilirken, her bitin önemli olduğu profesyonel amaçlı uygulamalar için ise kayıpsız yaklaşımlar kullanılır.
Görüntü verisi sıkıştırma alanında, şekiller ve taranmış metin görüntüleri gibi düşük frekanslı görüntülerde kayıpsız, fotoğraflarda ise genellikle kayıplı sıkıştırma kullanılır.
Hareketli görüntü (video) sıkıştırma alanında, ses verisi sıkıştırma alanında olduğu gibi, profesyonel amaçlı bazı uygulama alanları haricinde genellikle kayıplı sıkıştırma kullanılır.
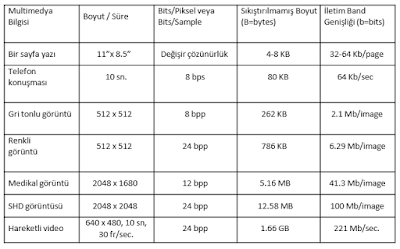
Sıkıştırılmamış çoklu ortam veri türleri ve ihtiyaç duyulan saklama alanları aşağıdaki tabloda verilmiştir.
Tablodaki veriler; görüntü, ses ve video işaretleri için çok büyük alanlara ihtiyaç duyulduğunu açıkça ortaya koymaktadır. Saklamak için yeterli alan olsa bile fazla sayıda görüntünün aktarılması veya videonun gerçek zamanlı gösterilmesi, transfer hızının düşük ve bant genişliğinin yetersiz olması sebebiyle mümkün değildir. Bunun için tek çözüm sıkıştırmadır. Bilgilerin saklanmadan ve gönderilmeden önce sıkıştırılması ve alıcıda tekrar açılarak orijinal bilginin elde edilmesi gerekir.
Şimdiye kadar sıkıştırmanın ana sebeplerinin, aktarmanın hızlandırılması ve saklama alanlarının daraltılması olarak iki tane olduğuna dikkat çekildi. Ancak sıkıştırmanın bazı alt hedefleri de mevcuttur. Bunlar;
- İşlemci ve bellek kullanımının minimuma indirilmesi
- Aktarma hatalarının etkilerinin azaltılması
- Görüntü sıkıştırmada yapılan temel işlem içerisindeki gereksiz ve ihtiyaç duyulmayan bilgilerin ortadan kaldırılmasıdır.
GEREKSİZ VE İHTİYAÇ DIŞI BİLGİLER
Görüntü dosyalarının yapısı gereği içerisinde ihtiyaç dışı ve gereksiz bilgi bulunur. Bu bilgilerin boyutunun çok büyük olması sebebiyle aktarma ve saklama problemi belirir. Sıkıştırma esnasında bu fazlalıklar atılırken orijinal bilgiden çok fazla uzaklaşmamaya özen gösterilir. O halde bu fazlalıkların nereden kaynaklandığını inceleyelim.
- Uzaysal fazlalık : Komşu pikseller arasındaki ilişkidir. Çoğu görüntülerde yan yana pikseller arasında keskin geçiş yoktur. Sıkıştırma yapmadan evvel, birbiriyle ilişkili pikseller (özellikle yan yana olanlar) tespit edilir.
- Spektral fazlalık : Farklı renk bileşenlerinin birbirleriyle olan ilişkileridir. Renk bileşenleri farklı bile olsa çoğunlukla birbirleriyle ilişkilidir.
- Anlık fazlalık : Video için birbirini takip eden çerçeveler arasındaki ilişkidir. Birbirini takip eden çerçeveler arasında çok büyük fark yoktur. Sadece hareket eden bölüm kadar fark vardır ve diğer bölümler hemen hemen aynıdır. Sıkıştırma işlemi içerisinde bu aynı bölümler fazlalık olarak değerlendirilir.
- Algılanabilen fazlalık : İnsanın görme sistemi her şeyi eşit olarak algılamaz. Uzaysal, spektral ve anlık kısıtlamalara bağlı kalarak görüntüde bazı gereksiz bilgiler atılabilir. İnsan gözü bu küçük değişimi algılamayacaktır.
Bir görüntü içerisindeki gereğinden fazla ve önemsiz bilgiler, piksellerin birbirleriyle olan bağlılaşımıyla doğru orantılıdır. Dolayısıyla bu fazla ve gereksiz bilgiler ne kadar fazla olursa sıkıştırma oranı da o kadar fazla olacaktır.
SIKIŞTIRMA METODLARI
Sıkıştırmanın sınıflandırılması bazı bilim adamlarına göre farklılık göstermekle birlikte genel olarak kayıplı ve kayıpsız sıkıştırma teknikleri olarak ikiye ayrılmıştır.
Kayıpsız Teknikler (Redundancy Reduction)
a. Huffman Kodlaması
b. Aritmetik Kodlama
c. Dictionary Tabanlı Kodlama (LZ77, LZ78, LZW)
d. Koşu Uzunluğu Kodlaması (RLE)
Kayıplı Teknikler (Entropy Reduction)
a. Skalar Kuantalama (PCM)
b. Öngörülü Kodlama (DPCM, Delta Modülasyonu)
c. Vektör Kuantalama (VQ)
d. Dönüşüm Kodlaması (DCT, WT)
e. Altband Kodlaması
f. Kesirsel (Fraktal) Kodlama (IFS ve PIFS)
DCT (Discrete Cosine Transform), Ayrık Kosinüs Transform (JPEG)
Durağan ve hareketli resimler için en sık kullanılan yöntem DCT (Discrete Cosine Transform), ayrık kosinüs transformudur. DCT ile bir görselin ayrık kosinüs bileşenleri üzerinde kuantalama (Bir fonksiyonun ayrik değerlerinin 0 ve 1 lere denk düşürülmesi diğer bir ifadeyle sonsuz ve sürekli bir analog sinyalin sonlu ve ayrık bir dijital sinyale benzetilmesi, dönüştürülmesi.) yaparak sıkıştırma işlemini gerçekleştirmiş oluyoruz. DCT ‘nin uygulandığı görsel formatları JPEG ve MPEG dir. DCT aynı zamanda TV teknolojisinde de kullanılmaktadır.
DCT' nin genel yapısı aşağıdaki gibidir.
1 boyutlu DCT formülasyonu:
Koşullar:
DCT’ nin izlediği yol
- Görsel 8×8 bloklara ayrılır.
- Soldan sağa yukarıdan aşağıya bir yön izleyerek her bir bloğa DCT dönüşümü uygulanır.
- Her blok kuantalanarak sıkıştırılır.
- İstenildiği zaman, IDCT ile genişletme yapılır.
8×8 bloklar için dönüşüm matrisi aşağıdaki gibidir.
Görselimizi temsilen bir M matrisi tanımlayalım.
DCT dönüşümü;
𝐷=𝑇 * 𝑀 * 𝑇′ formülü ile elde edilir.
M matrisinin T ile çarpılması satırlarda DCT dönüşümünü T’nin transpozu ile çarpımı da kolonlarda DCT dönüşümünün tamamlanmasını sağlıyor.
D matrisinin (0,0) elemanı en düşük frekanslı imaj bloklarını (7,7) elemanı ise en yüksek frekanslı imaj bloğunu vermektedir. İnsan gözü düşük frekansları görmek için hassas bir yapıya sahiptir. Daha sonraki bölümlerde yüksek genlikli değerleri matriste sol üst bölüme taşımak için kodlama yapacağız.
Kuantalama
- 8×8’lik DCT katsayılar matrisi oluştuktan sonra kuantalama yaparak sıkıştırma işlemini gerçekleştireceğiz.
- Sıkıştırma oranı arttıkça kalite azalır.
- JPEG görüntü yapısı itibariyle bizlere farklı seviyelerde görüntü sıkıştırma oranları belirleyebilme rahatlığı sağlıyor.
- %50’lik bir sıkıştırma oranı kalite ve boyut bakımından en optimize seçenektir. Aşağıda sıkıştırma derecesi %50 olan kuantalama matrisi verilmiştir.
Ben, %50’lik kalite oranında kuantalama matrisi kullanacağım. Bir fonksiyonun ayrık değerlerinin belli bir aralıkta incelenmesine kuantalama (nicemleme) denir.
Kuantalama işleminde bütün değerler belli bir aralığa indirgendiği için kayıp vardır. Örneğin 0 ile 50 arasındaki bütün değerler herhangi bir a değerine 50 ile 100 arasındaki tüm değerler de b gibi herhangi bir değere karşılık gelebilir.
Yukarıdaki bölüm ifadesinde D matrisindeki her eleman Q kuantalama matrisindeki her elemana eleman eleman bölünür ve round fonksiyonu bölüm ifadesini en yakın tam sayıya yuvarlar.
Aşağıda DCT dönüşümü yapılmış C matrisi bulunmaktadır.
Kodlama
Kuantalanmış C matrisine uygulayacağımız bu işlemde her bir matris elemanı binary dataya dönüştürülür ve o şekilde saklanır. Kuantalamadan sonra JPEG formatındaki görsellerin matrislerinde sıfır tekrarları çokça görülür. Bu durumda daha kolay ve kısa sürede sıkıştırma işleminin gerçekleşmesini sağlar.
Kodlama işlemi matriste zig zag çizilerek yapılır. Zigzag kodlama yapılmasının amacı düşük frekanslı katsayıları matrisin üst tarafına taşımaktır.
Ters DCT (IDCT)
Sıkıştırdığımız matrisi şimdi ters dönüşüm yaparak orjinal haline getirmeye çalışacağız. Ne kadar iyi kuantalama yapılsa da görüntü sıkıştırma işlemlerinde kayıp kaçınılmazdır. Bunun sebebi de geri dönüşüm yapılırken uygulanan interpolasyon işlemidir.
İnterpolasyon, birbirinden farklı değerler arasında yakın değerlere ilişkin en uygun değerler üretme işlemidir. Lineer, dairesel vb. bir dizi interpolasyon algoritması bulunmaktadır. Şimdi adım adım uyguladığımız DCT dönüşümünün tersine çevirelim.
İlk önce elde ettiğimiz C matrisini Q kuantalama matrisi ile çarparak, DCT matrisine ulaşacağız. Bu matrise R matrisi diyelim.
Çarpım sonucu elde ettiğimiz R matrisi aşağıdaki gibidir.
R matirisini transform matrisinin önce transpozu ve sonrasında kendisiyle çarpıp matris elemanlarını en yakın tam sayıya yuvarlıyoruz.
𝑀2=𝑟𝑜𝑢𝑛𝑑(𝑇' * 𝑅 * 𝑇)
M2 matrisi sıkıştırılmış görselin tekrar genişletilmesiyle elde edilmiş matristir. Şimdi orjinal matrisi ile genişletilen matrisi karşılaştıralım.
Yukarda yapmış olduğumuz işlemlerin çıktıları görünmektedir.
MATLAB UYGULAMASI - ÖNBİLGİ
Resimleri temel olarak dört türe ayırabiliriz:
- İkilik resimler
- İndekslenmiş resimler
- Gri seviye resimler
- Gerçek-renkli resimler
NOT: Resimler uint8, uint16, int16, single veya double tipi olabilirler.
Uint tipinde değerler [0 ile 255] aralığında değişirken, Double tipinde değerler [0 ile 1] aralığında değişir.
Aşağıda bir double değerlerden bir A matrisi verilmiştir.
Double tipinde değerler [0 ile 1] aralığında değişir. Aşağıda bir double değerlerden bir A matrisi verilmiştir.
A=
0.2275 0.2235 0.2392 0.4431 0.6784 0.7412
0.2275 0.2235 0.2314 0.4275 0.6706 0.7216
0.2314 0.2314 0.2235 0.3922 0.6588 0.7059
0.2314 0.2314 0.2196 0.3490 0.6314 0.7098
0.2275 0.2314 0.2196 0.3137 0.6157 0.7176
0.2314 0.2353 0.2235 0.2667 0.5490 0.7216
0.2275 0.2353 0.2353 0.2314 0.4235 0.6824
0.2275 0.2353 0.2392 0.2235 0.3294 0.6353
0.2314 0.2353 0.2353 0.2275 0.2549 0.5451
0.2275 0.2275 0.2353 0.2392 0.2235 0.3922
Buradan şöyle bir sonuç çıkarmalıyız. Resimlerde çalışırken hangi tür olduğunun yanısıra elemanlarının sınıfı da (veri tipi) önemlidir. DCT ile Görüntü Sıkıştırma Metodunda fonksiyonlarımız double değerlerde çalıştığı için yüklediğimiz görüntünün tipi uint de olsa single da olsa biz bunları double’a dönüştürmemiz gerekir.
Bunun içinde X = im2double(img); komutunu kullanırız.
Gelelim Matlab uygulamasına :)
clc, clear all;
resim=imread('image/ben.jpg'); %Görseli Okuyoruz
resim=double(resim);
satir_sayisi=size(resim,1);
kolon_sayisi=size(resim,2);
satir_blok_sayisi=floor(kolon_sayisi/8); %Satırlar 8*8 lik Bloklara ayırılıyor.
sutun_blok_sayisi=floor(satir_sayisi/8); %Sütunlar 8*8 lik Bloklara ayırılıyor.
s8=[];
for k=1:3 %RGB (Red,Green Blue) 3 Boyutlu Matristir. 3 Boyuta da DCT Uygulayacağız.
for i=1:satir_sayisi
satir_DCT=dct(resim(i,:,k)); %Satırlara DCT Uygulandı.
s8(i,:,k)=idct(satir_DCT(1:satir_blok_sayisi),satir_sayisi); % Ters DCT Uygulandı.
end
end
s8y=[];
for k=1:3
for i=1:kolon_sayisi
kolon_DCT=dct(s8(:,i,k)); %Kolonlara DCT Uygulandı.
s8y(:,i,k)=idct(kolon_DCT(1:sutun_blok_sayisi),kolon_sayisi); %Ters DCT Uygulandı.
end
end
%Resimleri Gösteriyoruz.
subplot(1,2,1);image(uint8(resim)); title('Orjinal Resim');
subplot(1,2,2);image(uint8(s8y)); title('Sıkıştırılmış Resim');Sonuç aşağıdaki gibidir.
İlk resmimiz 17 KB iken sıkıştırılmış resmimiz 4 KB inmiştir. Yani %76,4 küçülmüştür.
Resimdeki maksimum sinyal gürültü oranını (PSNR) yi hesaplayacak olursak;
DIF=imsubtract(uint8(resim),uint8(s8y));
mse=mean(mean(DIF.*DIF));
rmse=sqrt(mse);
psnr=20*log(255/rmse);
disp('PSNR');
disp(psnr);Resmimizin
İlk kanalında(RED) 78.7345 dB,
İkinci kanalında(BLUE) 79.6097 dB,
Üçüncü kanalında(GREEN) 82.8656 dB gürültü çıkmıştır.
- [message]
- NOT
- Matlabda Blok İşleme Yöntemi ile de görüntü sıkıştırma yapılabilir. Bunun için aşağıdaki linkleri sırasıyla incelenip mantığı kavranırsa daha pratik ve daha kaliteli sonuçlar alınabilir.
1- Block Processing Large Images
2- Discrete Cosine Transform