Fourier serileri ve MATLAB da periyodik sinyallerin fouirer seri açılımını bulmak

ÖZET

Fransız fizikçi ve matematikçi Joseph Fourier, sinüsoidal olmayan ama periyodik bir fonksiyonun sinüs ve kosinüslerin sonsuz toplamı biçimde yazılacağını ifade etmiştir. Daha doğrusu sinüsoidal olmayan periyodik bir fonksiyonun genliği ve frekansı birbirlerinden farklı olan sinüsoidal dalgalara ayrılabileceğini belirtmiştir.

Jean-Baptiste Joseph Fourier (1768 - 1830)

Joseph Fourier bu teoremi ilk olarak metal çubuk veya levhadaki ısı denklemlerinin çözümü için kullanmıştır. Isı denklemi diferansiyel bir denklemdir ve çözümü zordur. Fourier bu denklemi basitleştirerek sinüs ve kosinüsleri katsayılarla birbirine ekleyerek karmaşık bir ısı kaynağı oluşturmak hedefindeydi. Bu denklemlerin belli katsayılarla sonsuz toplamına da Fourier Serisi olarak adlandırılmaktadır.

Ancak J. Fourier bu teoremi ısı denklemlerine uyguladıktan sonra görülmüş ki teorem, daha geniş periyodik fonksiyonlara uygulanabilmekte. Euler, Jean le Rond d'Alembert ve Daniel Bernoulli’de bu teoremi daha da geliştirerek Fourier serilerinin modern halini almasını sağlamışlardır.

Bir fonksiyonun Fourier serisine açılabilmesi için gerekli şartlar:

• Fonksiyonun bir periyot değeri olmalı ki belli periyot aralıklarında tekrarlanmalı.
• Sonlu sayıda süreksizlik barındırmalı,
• Sonlu sayıda maksimum ve minimum noktaları olmalı ve fonksiyonun ortalama değeri de bir sonlu değer almalı

Fonksiyon şartları sağlandığı zaman şu şekilde açılır;

Seriyi daha da açarsak;

Burada A0, fonksiyonun ortalama değeridir. Sabit bir değerdir. Örneğin bir gerilimin veya akımın harmonik analizini yapacaksak gerilim veya akımın ortalama değeri A0 :

Sistemimiz sinüs ise ortalama değer sıfırdır. Bazı literatürlerde sabit terim A0/2 olarak da alınır. Eğer böyle alınırsa ortalama değeri yani sabit terimi bulurken formülün başındaki 1/T yerine 2/T yapmamız gerekmektedir.

“1” indisi ile gösterilen birinci terime, temel bileşen adı verilir.  Temel bileşen aynı zamanda tam sinüsoidal dalgaya karşılık düşen dalgayı  belirler. 2, 3, 4,..., n indisi ile gösterilen bileşenlere ise harmonik adı  verilmektedir. A1, A2, A3,….., An, B1, B2, B3,….., Bn  f(t) fonksiyonunun Fourier katsayılarıdır. Yine serideki n değeri ise 1, 2, 3,...,n (pozitif tam sayı) şeklinde giden harmonik mertebesidir.  

Harmonik analizinde Fourier serisinin önemi

Bilindiği gibi elektrik şebekemiz sinüs şeklinde. Günümüzde güç elektroniği teknolojisinin gelişmesiyle yarı iletken elemanları çok kullanır olduk. Yarı iletken elemanlar şebekemizde harmoniğe sebep olabilirler. Ayrıca şebekenin yükünün büyük bir bölümünü elektrik motorları kapsamakta. Yine elektrik motorları ve motor sürücüleri (içinde bir çok yarı iletken bulundurması sebebiyle) şebekeden harmonik içerikli akımlar çeker.

Sistemin ne tür harmonikler yarattığını öğrenmek çok önemli. Harmonikli fonksiyonlar kompleks fonksiyonlardır ve çözümü zordur. İşte burada yardımımıza Fourier analizi koşar. Harmonikli fonksiyonun nerelerde kaçıncı harmonik yaptığını öğrenmemiz gerekebilir. Özellikle şebekede ve transformatörlerdeki harmonik bileşenlerini analiz etmek için Fourier serisini kullanıyoruz. Fourier serisi sayesinde harmonikli bir gerilim veya akım fonksiyonunu (fonksiyon periyodik tabiki ama harmonikli yani bozuk bir sinüs gibi düşünebiliriz) farklı genlikte ve frekansta sinüs ve kosinüslerin toplamı biçiminde yazarak hangi anda nasıl bir harmonik yaptığını öğrenebiliriz.

Fourier'in bize seriler konusunda anlatmak istediği bu kadar. Şimdi yukarıdaki teorik bilgiyi MATLAB kullanarak gerçeğe dönüştürelim

UYGULAMA

Şimdi öncelikli olarak -1 ile 1 arasında, periyodu 2 olan ve tepe noktası +1 ile 0 arasında değişen kare dalga çizdirelim. Daha sonra bu işaretin formulunu fourier serisi kullanarak hesaplayalım.

t = linspace(-2, 2, 500);
T=2;
ft = (square(2*pi*t*(1/T))+1)/2;

Yukarıdaki kodun çıktısı tam olarakta sözel olarak ifade ettiğimiz işaret olmalı. Burada square fonksiyonu -1 1 arasında değişen kare dalga oluşturuyor. Biz de bunu 1 0 arasına çekmek için 1 ekleyip 2'ye böldük. Oluşan işaret aşağıdadır.

Amacımız yukarıda yer alan kare dalgayı cosinus ve sinus fonksiyonlarının toplamı şeklinde yazmaktır. Bunun için Fourier serisi katsayılarını belirlememiz yeterlidir. an ve a0 için aşağıdaki formulleri kullanıyoruz.

Burada birşeye dikkatinizi çekmek isterim. n yerine ne verirsek verelim an 0 olacaktır. Haliyle bu işaretimizin cosinus bileşeni yoktur. Bu bize işaretin tek olduğu bilgisini verir. Siz de Fourier serisine açma işlemine başlamadan önce işaretin tek mi çift mi olduğunu belirlemelisiniz. Bu size ciddi bir kolaylık sağlar. Eğer işaret çift ise sinus bileşeni olmayacak tek ise de cosinus bileşeni olmayacak.

an katsayısının 0 olduğunu gördükten sonra sıra bn katsayılarını bulmaya geldi. Onu da aşağıdaki formül ile buluyoruz.

Burada ufak düzenlemeler yaptıktan sonra işaretimizin temsili aşağıdaki şekilde olacaktır.

İşin teorisini ve matematiğini hallettikten sonra şimdi bunu kendi gözümüzle görelim. Yapmamız gereken en altta yer alan sinus ifadelerini toplayıp gerçekten de ilk işaretimize benzeyip benzemediğini görmek. Hemen deneyelim.

t = linspace(-2, 2, 500);
T=2;
ft = (square(2*pi*t*(1/T))+1)/2;
fs = 1.0/2 + (2/pi)*sin(pi*t)
plot(t,ft,'LineWidth',2)
hold on
plot(t,fs,'LineWidth',2)

Şimdilik sadece DC bileşen olan 1/2 ve ilk katsayıyı ekledik. Yukardaki görüntüyü elde etmemiz gerekiyor.

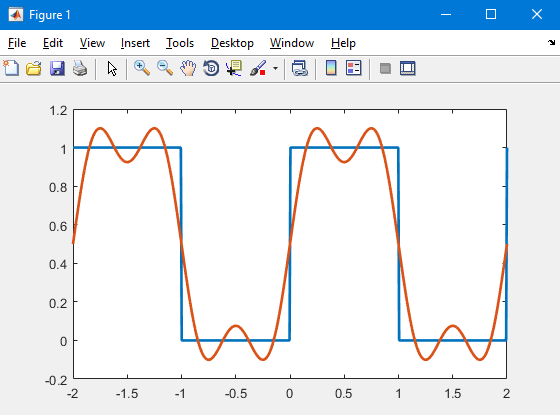
Fourier serisi ile oluşturduğumuz fs fonksiyonumuza bir katsayı daha eklediğimizde iyice yaklaşmaya başladığını hissediyoruz.

fs = 1/2 + (2/pi)*sin(pi*t) + (2/(3*pi))*sin(3*pi*t)

Olayı anladığımız üzere artık bunun için bir fonksiyon yazıp istediğimiz kadar katsayıyı toplayıp gerçek işarete yakınlaşabiliriz.

M=10 İÇİN

t = linspace(-2, 2, 500);
T=2;
ft = (square(2*pi*t*(1/T))+1)/2;
a0=1/2;
fs=0;
M=10;
for i=1:2:M
    fs=fs+(2/(i*pi))*sin(i*pi*t);
end
fs=a0+fs;

plot(t,ft,'LineWidth',2)
hold on
plot(t,fs,'LineWidth',2)

M=50 İÇİN

M=10000 İÇİN

NOT: Fonksiyonun yükselme ve alçalma noktalarında oluşan diklik katsayıyı ne kadar artırırsak o kadar sürekli olacaktır. Buna Gibbs olayı deniliyor. Mümkün olduğunca azaltmamız gerekiyor. Son olarakta 10000 katsayıdan oluşan işareti çizdirdim. Artık orjinal işaretimizin neredeyse aynısı oldu.

Fourier serilerini daha detaylı incelemek isteyenler aşağıdaki pdf e bakabilirler.